[프로그래머스 5단계]알고리즘 38. 하노이 탑

문제 출처는 프로그래머스 알고리즘 연습 에서 볼 수 있습니다!(https://programmers.co.kr/learn/challenges)

문제 38. 하노이 탑

하노이의 탑은 대표적인 퍼즐의 일종입니다. 세 개의 기둥이 있고 맨 왼쪽의 기둥에는 원판의 크기 순서대로 N개가 쌓여 있습니다.

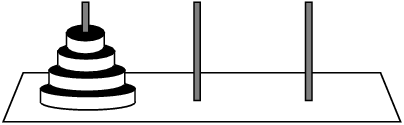
이렇게 쌓여 있는 원판을 가장 오른쪽 기둥으로 모두 옮겨야 합니다.
단, 한 번에 원판을 하나씩 이동시킬 수 있고, 큰 원판을 작은 원판 위에 쌓을 수 없습니다.

N개의 원판은 총 2N -1 번의 과정을 거쳐 이동할 수 있습니다. 하지만 어떠한 과정으로 원판을 옮겨야 2N -1 번만에 옮길 수 있는지는 아직 모릅니다. 원판이 N개 있을 때, Hanoi 함수에서 어떠한 과정으로 2N -1 번만에 옮길 수 있는지 과정을 리턴하세요.

리턴값의 표기 방법은 다음과 같습니다.

• 3개의 기둥은 순서대로 각각 1, 2, 3번으로 표기합니다.
• 원판을 기둥1에서 기둥3으로 이동했다면 [1, 3]으로 표기합니다.
• 원판을 기둥3에서 기둥1로 이동했다면 [3, 1]로 표기합니다.

이러한 이동 순서를 담는 배열을 리턴하면 됩니다. 예를들어 N이 2라면 아래 그림과 같이 옮길 수 있으므로

리턴값은 [ [1,2], [1,3], [2,3] ]입니다.

class Hanoi {

    public int[][] hanoi(int n) {

        // 2차원 배열을 완성해 주세요.

        int[][] answer = null;

        return answer;

    }

    // 아래는 테스트로 출력해 보기 위한 코드입니다.

    public static void main(String[] args) {

        Hanoi h = new Hanoi();

        System.out.println(Arrays.toString(h.hanoi(2)));

    }

}

풀이:

하노이 탑은 대표적인 재귀 문제이다. 이 문제의 핵심은 한 기둥에서 한 기둥으로 옮기는 작업을 하나의 덩어리로 보는 것이다. 그러니까 우리의 목표는 A->C로 옮기는 것이다. 예제를 보았을 때 크게 작업을 다음과 같이 나눌 수 있다. 

1. 가장 큰 원반을 제외한 나머지 원반을 A->B로 옮긴다.

2. 가장 큰 원반을 A->C로 옮긴다.

3. B에 있는 원반들을 B->C로 옮긴다.

감이 대충 오는가? 무슨 문제 풀이를 이따위로 해! 라고 성낼수도 있을 것 같다. 때로는 문제를 크게, 대충 보아야 답이 보일 때도 있다. 그러니 바로 코드로 살펴보자.

class Hanoi {

void move(List<int[]> moveList, int n, int from,int by, int to){

if (n==1)

moveList.add(new int[]{from, to});

else{

move(moveList, n-1, from, to, by);

moveList.add(new int[]{from, to});

move(moveList, n-1, by, from, to);

}

}

    public int[][] hanoi(int n) {

        // 2차원 배열을 완성해 주세요.

        

List<int[]> moveList = new ArrayList<>();

move(moveList, n, 1, 2, 3);

        return moveList.toArray(new int[moveList.size()][]);

    }

    // 아래는 테스트로 출력해 보기 위한 코드입니다.

    public static void main(String[] args) {

        Hanoi h = new Hanoi();

        System.out.println(Arrays.toString(h.hanoi(2)));

    }

}

우리가 살펴보아야 할 코드는 move 메소드이다. 여기서 move 메소드의 작업을 크게 살펴보면 다음과 같다. if부분은 재귀함수의 탈출 부분이다. 최종적으로 마지막 원반을 from -> to 즉 A->C로 옮기는 작업이다. else 부분은 다음과 같이 해석할 수 있다.

1. n-1번째 해당하는 원반까지 모두 from -> by [A -> B]

2. n번째 원반을 from -> to [A -> C]

3. B로 옮긴 n-1개의 원반들을 모두 by -> to [B -> C]

아까 설명한 부분과 상당 수 일치한다. 정말로 이게 될까?라고 생각하는 분들은 한 번 결과를 출력 시켜보기를 권한다.  이 코드의 문제는 객체를 2^N -1 + @(리스트, 나중에 Array 변경)개 만큼 생성해낸다는 건데, 이는 static 변수를 활용하여 바꿀 수 있다. 바꾼 코드는 다음과 같다.

class Hanoi {

private int COUNT = 0;

private void move(int [][] arr, int n, int from, int by, int to){

if (n == 1){

arr[COUNT][0] = from;

arr[COUNT][1] = to;

COUNT += 1;

}else {

move (arr, n-1, from, to, by);

arr[COUNT][0] = from;

arr[COUNT][1] = to;

COUNT += 1;

move(arr, n-1, by, from, to);

}

}

    public int[][] hanoi(int n) {

        // 2차원 배열을 완성해 주세요.

        int[][] answer = null;

int N = (int)Math.pow(2, n) - 1;

answer = new int[N][2];

move(answer, n, 1, 2, 3);

        return answer;

    }

    // 아래는 테스트로 출력해 보기 위한 코드입니다.

    public static void main(String[] args) {

        Hanoi h = new Hanoi();

        System.out.println(Arrays.toString(h.hanoi(2)));

    }

}